在Java编程中,计算e的次方是一个常见的数学运算需求,e作为自然对数的底数,约等于2.71828,在科学计算、金融建模、机器学习等领域有着广泛应用,要实现Java中e的次方计算,开发者需要掌握Java提供的数学工具库,理解不同方法的适用场景,并注意数值计算的精度与性能问题,本文将系统介绍Java中计算e次方的多种实现方式,包括核心方法、代码示例、注意事项及性能优化建议。
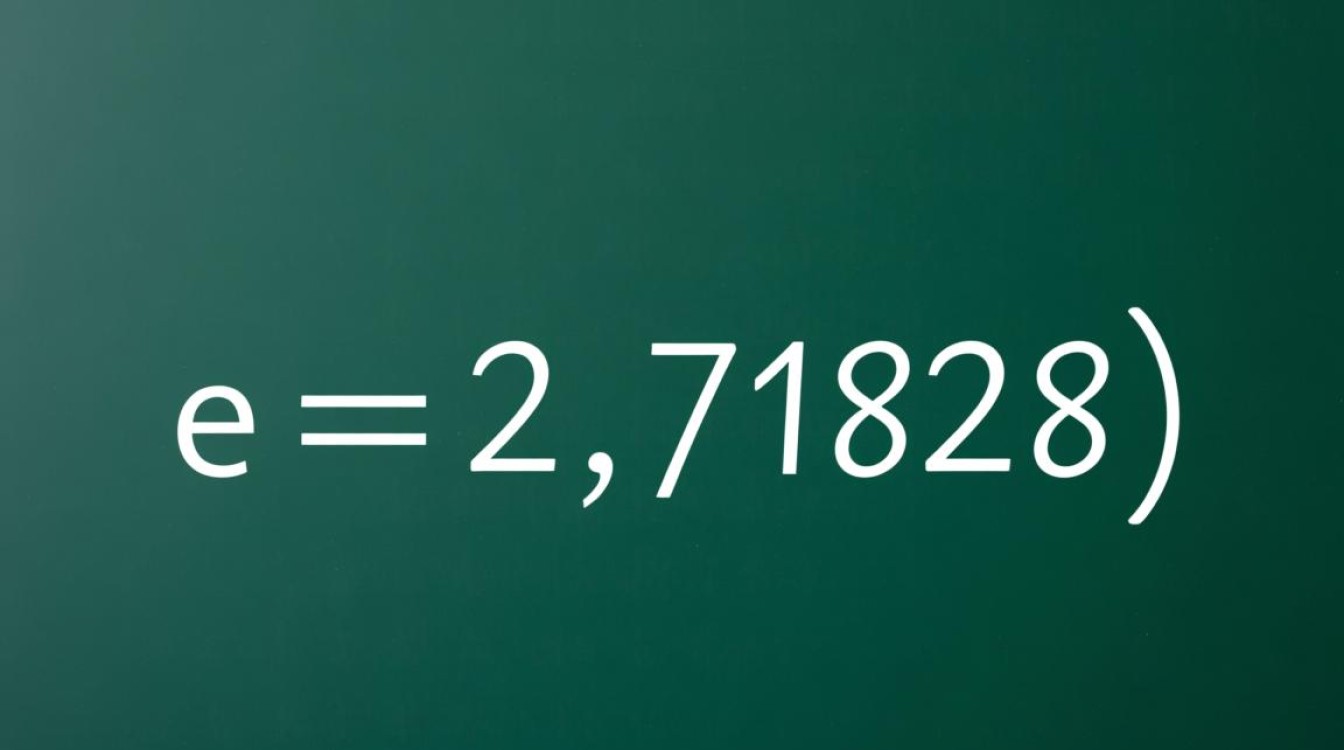
核心计算方法:Math.exp()
Java标准库中的Math类提供了exp()方法,专门用于计算e的指定次方,该方法接受一个double类型的参数x,返回e^x的值,其本质是自然指数函数的实现,计算e的2次方,只需调用Math.exp(2),系统会自动返回Math.E的平方值,该方法经过高度优化,底层采用泰勒级数展开或查表插值等算法,确保计算精度和效率,需要注意的是,exp()方法的参数范围有限,当输入值过大(如超过709)时,会导致结果溢出,返回Double.POSITIVE_INFINITY;而输入值过小(如低于-708)时,结果会趋近于0,返回0.0。
其他实现方式与替代方案
除了Math.exp(),开发者还可以通过自然对数ln()和幂运算pow()组合实现e的次方计算,由于e^x可以表示为Math.pow(Math.E, x),因此这种写法在功能上与Math.exp()等价,从性能角度看,Math.exp()直接调用硬件指令或优化算法,而pow()方法需要额外处理底数参数,因此在频繁调用场景下,exp()的效率通常更高,对于特殊场景,如需要自定义精度的计算,可以考虑使用BigDecimal类结合泰勒级数展开手动实现,但这种方法复杂度高且性能较差,仅适用于学术研究或极端精度需求。
代码示例与实际应用
以下通过具体代码示例展示e次方的计算方法,使用Math.exp()计算e的1.5次方:
public class ExponentialExample {
public static void main(String[] args) {
double x = 1.5;
double result = Math.exp(x);
System.out.println("e^" + x + " = " + result); // 输出:e^1.5 = 4.4816890703380645
}
}
若需通过pow()方法实现,代码如下:

double result = Math.pow(Math.E, x); // 结果与Math.exp(x)相同
在实际应用中,e次方常用于复利计算、概率分布等领域,计算连续复利时,若年利率为r,连续投资t年,本息和为Pe^(rt),可通过Math.exp(r * t)快速求解。
注意事项与边界处理
在使用e次方计算时,需特别注意数值边界和精度问题。Math.exp()的返回值是double类型,存在浮点数精度误差,对于高精度场景,建议使用BigDecimal并设置足够的小数位数,当输入x为NaN(非数字)或无穷大时,exp()会遵循IEEE 754标准返回NaN或无穷大,开发者需提前校验输入参数。
if (Double.isNaN(x) || Double.isInfinite(x)) {
throw new IllegalArgumentException("Invalid input for exponential calculation");
}
对于负指数计算,如e^(-2),结果为1/e^2,可直接调用Math.exp(-2),无需额外处理。
性能优化与替代库
在性能敏感的应用中,如高频交易或大规模科学计算,可考虑以下优化策略:1)避免重复计算,将结果缓存至变量;2)使用StrictMath.exp()替代Math.exp(),后者可能依赖平台特定的优化实现;3)对于近似计算,采用查表法或多项式近似,牺牲少量精度换取速度,若需更高性能,可引入第三方数学库如Apache Commons Math或EJML,这些库提供了更高效的指数函数实现,并支持并行计算。

Java中计算e的次方主要通过Math.exp()方法实现,该方法简洁高效,适用于大多数场景,开发者需掌握其边界行为和精度特性,并结合实际需求选择合适的实现方式,在复杂应用中,合理利用数学库和优化技巧,可以显著提升代码的性能和可靠性,通过深入理解e次方的计算原理,开发者能够更灵活地应对科学计算、工程建模等领域的挑战。


















