Java中如何准确运用求根公式求解一元二次方程？

Java中求根公式应用详解

在数学中,求根公式是解一元二次方程 ( ax^2 + bx + c = 0 ) 的标准方法，在Java编程语言中，我们可以通过编写一个简单的函数来实现这一计算，以下将详细介绍如何在Java中使用求根公式。

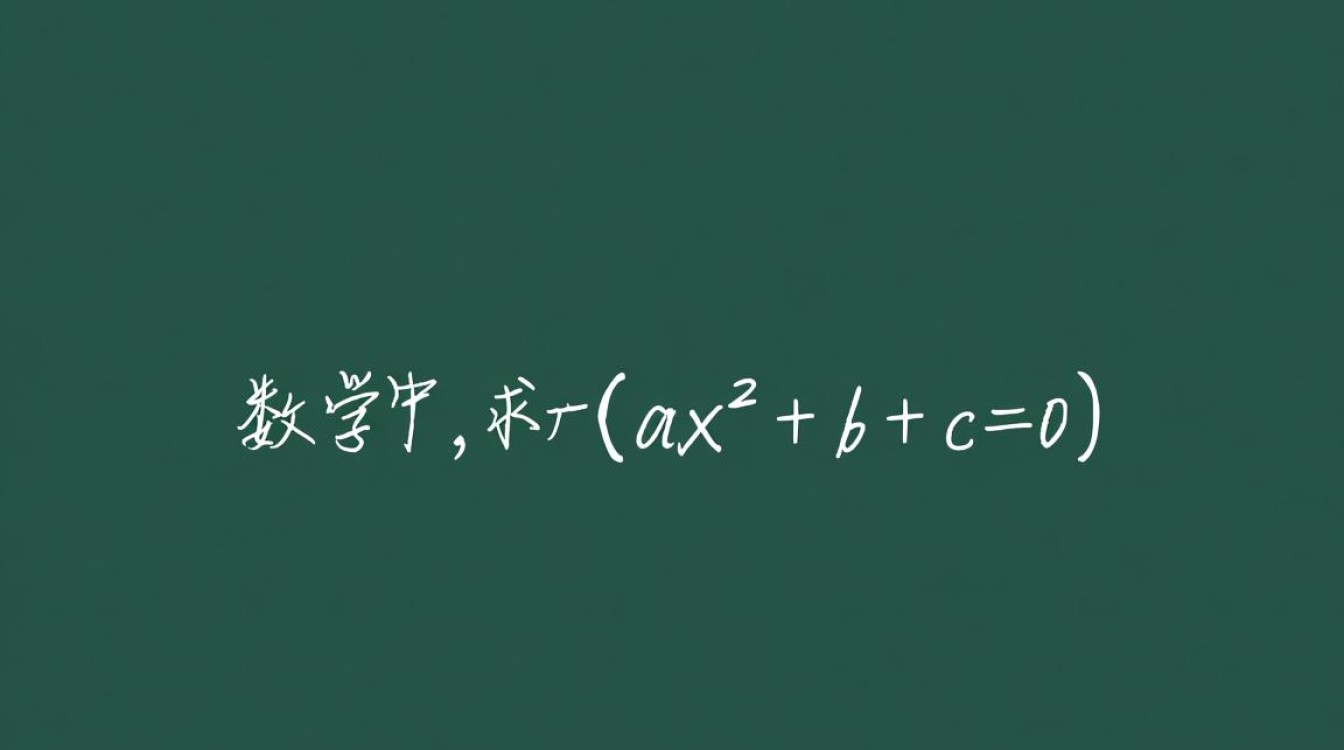
求根公式简介

一元二次方程的求根公式如下：

[ x = \frac{-b \pm \sqrt{b^2 – 4ac}}{2a} ]

( a )、( b )、( c ) 是方程中的系数，( \sqrt{b^2 – 4ac} ) 是判别式，用于判断方程的根的性质。

Java中实现求根公式

为了在Java中实现求根公式,我们需要编写一个函数，该函数接收三个参数 ( a )、( b )、( c )，并返回方程的两个根（如果存在的话）。

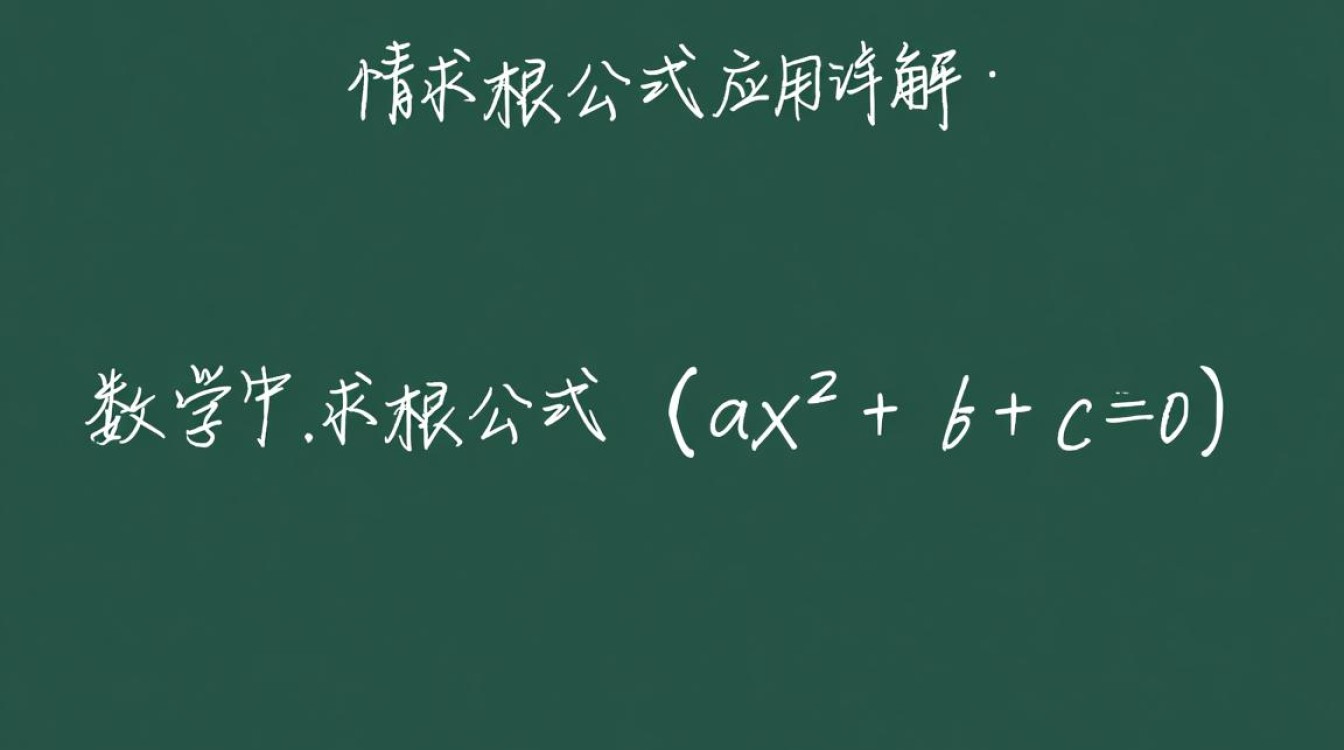
以下是一个简单的Java函数实现：

public class QuadraticEquationSolver {
    public static void main(String[] args) {
        double a = 1;
        double b = -3;
        double c = 2;
        double[] roots = solveQuadraticEquation(a, b, c);
        if (roots != null) {
            System.out.println("Root 1: " + roots[0]);
            System.out.println("Root 2: " + roots[1]);
        } else {
            System.out.println("No real roots exist.");
        }
    }
    public static double[] solveQuadraticEquation(double a, double b, double c) {
        double discriminant = b * b - 4 * a * c;
        double[] roots = new double[2];
        if (discriminant > 0) {
            roots[0] = (-b + Math.sqrt(discriminant)) / (2 * a);
            roots[1] = (-b - Math.sqrt(discriminant)) / (2 * a);
            return roots;
        } else if (discriminant == 0) {
            roots[0] = -b / (2 * a);
            return roots;
        } else {
            return null; // No real roots
        }
    }
}

注意事项

1. 判别式检查：在计算根之前，需要检查判别式 ( b^2 – 4ac ) 的值，如果判别式小于0，则方程没有实数根。

2. 异常处理：在实际应用中，可能需要处理一些异常情况，例如系数 ( a ) 不能为0，因为这会导致方程退化为一元一次方程。

3. 精度问题：由于浮点数的精度限制，计算过程中可能会出现微小的误差。

   

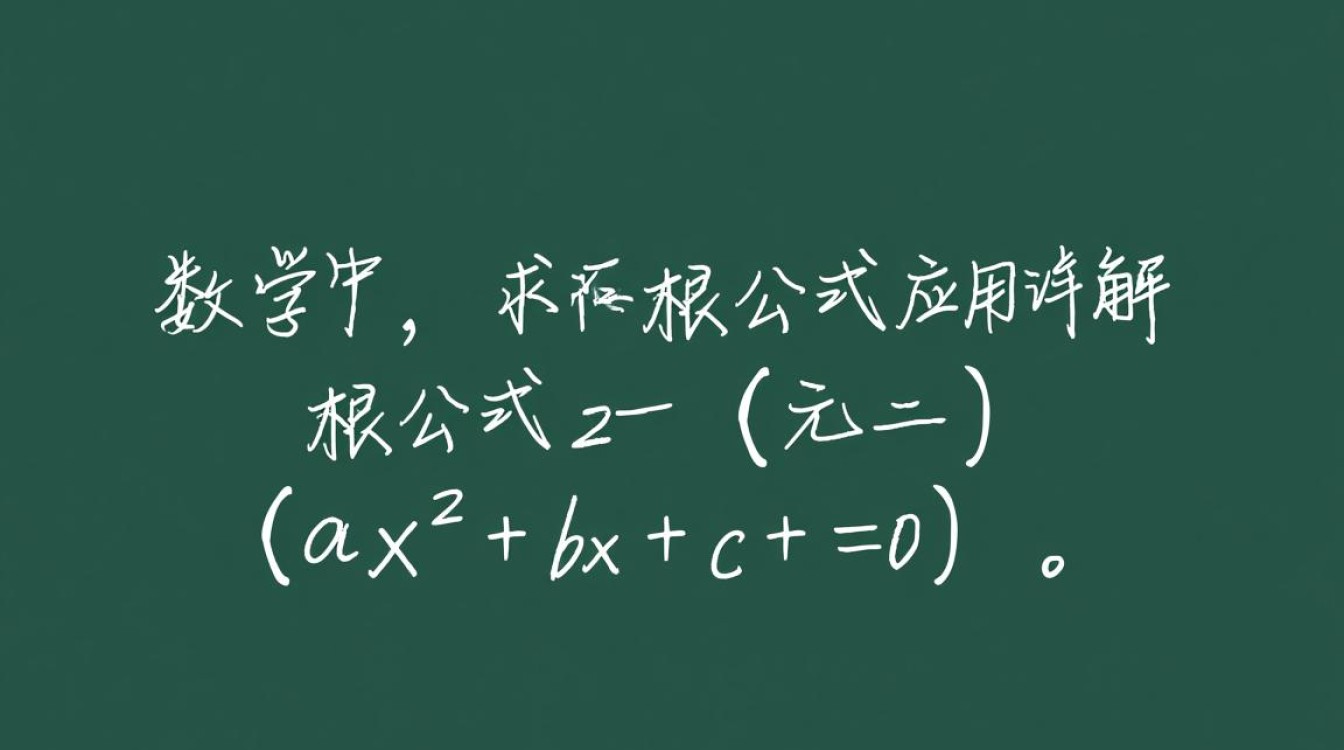
通过上述方法,我们可以在Java中实现一元二次方程的求根公式，了解并掌握这一方法对于进行数学计算和算法开发具有重要意义，在实际应用中，可以根据具体需求对上述代码进行优化和扩展。