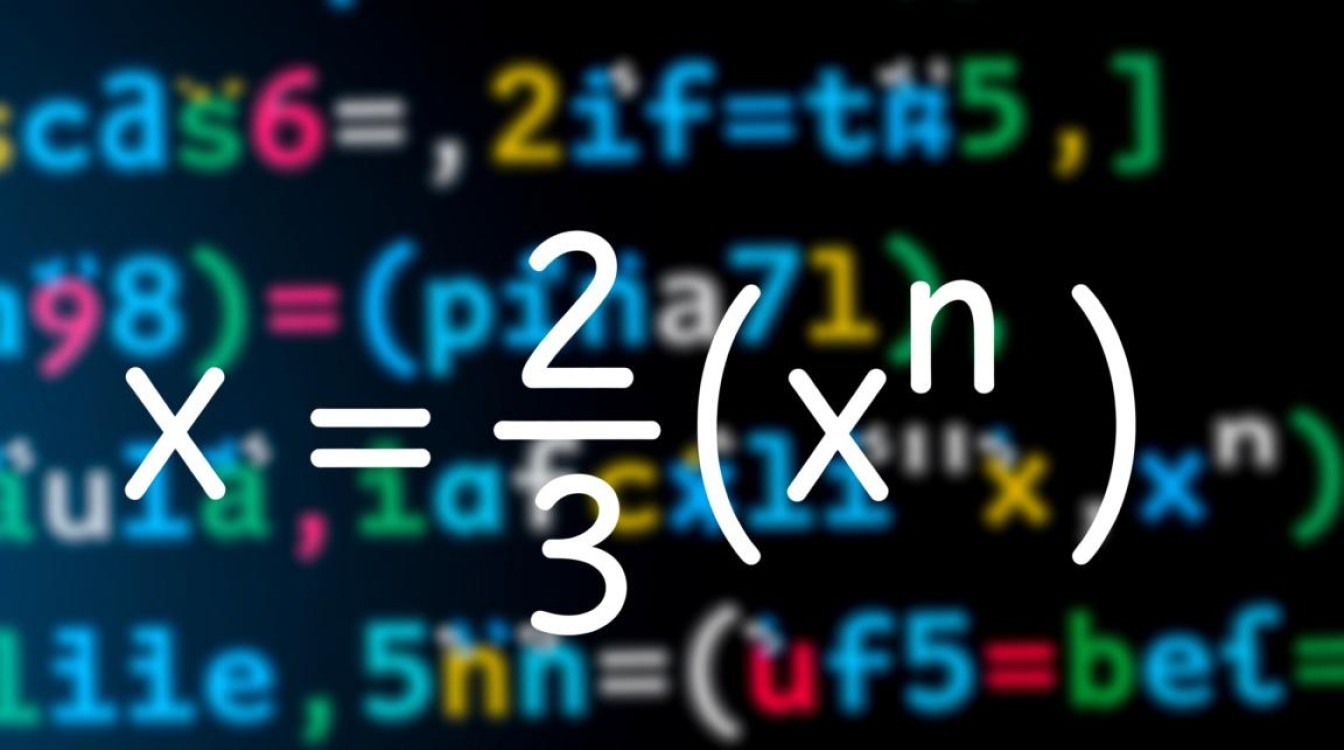在Java编程中,“幂运算”是一个常见的数学运算需求,指的是计算一个数的n次方,即a的n次方等于a乘以自身n次,Java提供了多种实现幂运算的方法,每种方法在性能、适用场景和易用性上各有特点,本文将详细介绍Java中实现幂运算的几种主要方式,包括基础循环实现、Math库方法、BigDecimal处理高精度需求,以及快速幂算法等,帮助开发者根据实际需求选择最合适的方案。

基础循环实现幂运算
对于初学者而言,最直观的幂运算实现方式是通过循环语句逐步累乘,这种方法逻辑简单,易于理解,适合小规模的幂运算需求,计算a的n次方,可以初始化一个结果变量为1,然后通过for循环或while循环,将结果乘以a,重复n次即可,以下是一个简单的实现示例:
public static double powerByLoop(double base, int exponent) {
double result = 1.0;
for (int i = 0; i < exponent; i++) {
result *= base;
}
return result;
}
这种方法的优点是代码清晰,无需依赖外部库,适合教学场景或简单的业务逻辑,其缺点也十分明显:时间复杂度为O(n),当指数n较大时(例如n=1000000),循环次数会急剧增加,导致性能低下,这种方法未对指数进行特殊处理(如负数或零),需要额外添加逻辑来完善功能,例如当指数为负数时,应计算其倒数的正数次方,当底数为0且指数为负数时,应抛出异常等。
使用Math库的pow方法
Java的标准库java.lang.Math提供了pow方法,专门用于执行幂运算,其方法签名为public static double pow(double a, double b),其中a是底数,b是指数,该方法底层采用了优化算法,性能远高于基础循环实现,能够高效处理各种指数情况(包括小数指数和负数指数),以下是使用示例:
double result = Math.pow(2.0, 3.0); // 计算2的3次方,结果为8.0
Math.pow方法的优点是高效且功能全面,适用于大多数科学计算和工程应用场景,需要注意的是,该方法返回值为double类型,可能会存在浮点数精度问题。Math.pow(2, 3)的结果是精确的8.0,但Math.pow(0.1, 2)的结果可能由于浮点数存储机制而出现微小误差(如0.010000000000000002),该方法对指数的范围也有限制,当指数过大或过小时,可能会返回Infinity或0,需要调用时注意边界条件。
BigDecimal处理高精度幂运算
在金融、财务等对精度要求极高的领域,double类型的浮点数误差是不可接受的,Java提供了java.math.BigDecimal类,用于高精度的十进制数运算,虽然BigDecimal本身没有直接提供幂运算方法,但可以通过结合pow方法(BigDecimal的pow方法接受int类型指数)和自定义逻辑来实现,以下是示例:

import java.math.BigDecimal;
public static BigDecimal powerByBigDecimal(BigDecimal base, int exponent) {
if (exponent == 0) {
return BigDecimal.ONE;
}
if (exponent < 0) {
base = BigDecimal.ONE.divide(base, MathContext.DECIMAL128);
exponent = -exponent;
}
return base.pow(exponent);
}
使用BigDecimal的优势在于可以精确控制计算精度,避免浮点数误差,计算1的平方,BigDecimal能够精确返回01,而Math.pow则可能存在精度偏差,但需要注意的是,BigDecimal的运算性能较低,且其pow方法仅支持整数指数,对于非整数指数需要通过其他方式(如对数运算)近似计算,实现复杂度较高,仅在精度要求严苛的场景下推荐使用。
快速幂算法优化性能
当指数非常大时(例如n=1000000000),无论是基础循环还是Math.pow方法都可能面临性能瓶颈,快速幂算法(Exponentiation by Squaring)是一种高效的幂运算优化算法,其核心思想是分治策略:将指数n分解为二进制形式,通过平方运算和乘法运算的组合,将时间复杂度从O(n)降低到O(log n),以下是快速幂的递归实现示例:
public static double fastPower(double base, int exponent) {
if (exponent == 0) {
return 1;
}
if (exponent < 0) {
base = 1 / base;
exponent = -exponent;
}
if (exponent % 2 == 1) {
return base * fastPower(base * base, exponent / 2);
} else {
return fastPower(base * base, exponent / 2);
}
}
快速幂算法通过递归或迭代方式,将问题规模不断减半,显著提升了大指数运算的效率,计算2的1000次方,快速幂仅需约10次运算(因为log₂1000≈10),而基础循环需要1000次运算,在实际开发中,快速幂算法常用于密码学、数值模拟等领域,需要处理大指数运算的场景,需要注意的是,递归实现的快速幂可能存在栈溢出风险(当指数极大时),此时可以改用迭代实现:
public static double fastPowerIterative(double base, int exponent) {
double result = 1.0;
long exp = exponent; // 使用long避免负数溢出
if (exp < 0) {
base = 1 / base;
exp = -exp;
}
while (exp > 0) {
if (exp % 2 == 1) {
result *= base;
}
base *= base;
exp /= 2;
}
return result;
}
幂运算的异常处理与边界条件
在实际应用中,幂运算需要考虑多种边界条件和异常情况,以确保程序的健壮性,常见的边界条件包括:
- 指数为0:任何非零数的0次方均为1,0的0次方在数学上无定义,Java中
Math.pow(0, 0)返回NaN。 - 底数为0且指数为负数:此时结果为无穷大(
Infinity),应抛出异常或进行特殊处理。 - 负数底数与小数指数:在实数范围内,负数的非整数次方可能为复数,Java中
Math.pow(-2, 0.5)返回NaN。 - 数值溢出:当结果超出
double类型的表示范围时,会返回Infinity或-Infinity,需提前检查或使用BigDecimal避免溢出。
在实现幂运算方法时,应根据业务需求添加相应的异常处理逻辑,

public static double safePower(double base, double exponent) {
if (base == 0 && exponent < 0) {
throw new ArithmeticException("0的负数次方无定义");
}
if (base < 0 && exponent % 1 != 0) {
throw new ArithmeticException("负数的非整数次方在实数范围内无定义");
}
return Math.pow(base, exponent);
}
总结与选择建议
Java中实现幂运算的方法多种多样,开发者应根据具体场景选择合适的方案:
- 基础循环:适用于教学演示或小规模指数运算,性能较差,不推荐生产环境使用。
- Math.pow:通用性最强,性能较好,适合大多数科学计算和日常开发,但需注意浮点数精度问题。
- BigDecimal:适用于金融等高精度需求场景,仅支持整数指数,性能较低。
- 快速幂:适用于大指数运算(如密码学、数值模拟),性能卓越,可递归或迭代实现。
在实际开发中,优先考虑Math.pow方法,其经过高度优化且能满足大多数需求,对于大指数运算,可采用快速幂算法;对于高精度场景,则选择BigDecimal,务必关注边界条件和异常处理,确保程序的稳定性和正确性,通过合理选择幂运算方法,可以有效提升代码的性能和可靠性。